Una serie de Fourier es una serie infinita que converge puntualmente a una función periódica y continua a trozos(o por partes). Las series de Fourier constituyen la herramienta matemática básica del análisis de Fourier empleado para analizar funciones periódicas a través de la descomposición de dicha función en una suma infinita de funciones senoidales mucho más simples (como combinación de senos y cosenos con frecuencias enteras). El nombre se debe al matemático francés Jean-Baptiste Joseph Fourier que desarrolló la teoría cuando estudiaba la ecuación del calor. Fue el primero que estudió tales series sistemáticamente, y publicando sus resultados iniciales en 1807 y 1811. Esta área de investigación se llama algunas veces Análisis armónico.
Es una aplicación usada en muchas ramas de la ingeniería, además de ser una herramienta sumamente útil en la teoría matemática abstracta. Áreas de aplicación incluyen análisis vibratorio, acústica, óptica, procesamiento de imágenes y señales, y compresión de datos. En ingeniería, para el caso de los sistemas de telecomunicaciones, y a través del uso de los componentes espectrales de frecuencia de una señal dada, se puede optimizar el diseño de un sistema para la señal portadora del mismo. Refierase al uso de un analizador de espectros.
Las series de Fourier tienen la forma:
 =
= ![\frac{a_0}{2} + \sum_{n=1}^\infty\left[a_n\cos\frac{2n\pi}{T}t + b_n\sin\frac{2n\pi}{T}t\right]](http://upload.wikimedia.org/wikipedia/es/math/5/5/8/558025a943d5a46c353605d33c6b6d2c.png)
Donde  y
y  se denominan coeficientes de Fourier de la serie de Fourier de la función
se denominan coeficientes de Fourier de la serie de Fourier de la función 
 y
y  se denominan coeficientes de Fourier de la serie de Fourier de la función
se denominan coeficientes de Fourier de la serie de Fourier de la función 
La serie de Fourier de una señal periódica esta definida por sus coeficientes A0, An, y Bn. En la siguiente entrada explicare como podemos hallar los coeficientes de Fourier de una señal cuadrada haciendo uso de Python, numpy, matplotlib, y sympy.
SYMPY
Sympy es una librería desarrollada en Python que permite realizar matemática simbólica. Esto quiere decir que podemos incluir variables matemáticas realizando operaciones algebraicas entre ellas. Sympy pretende ser un sistema algebraico computacional completo, libre y con una sintaxis limpia que siga los principios "pytonicos".
Sympy también es multiplataforma como Python por lo que puede ser instalado en cualquier distribución Linux, como en Windows o Mac OS X. Entre otras cosas Sympy ya tiene soporte para Python 3 lo cual representa un paso importante para la migración que se lleva a cabo en estos momentos.
Para instalar Sympy en Windows podemos hacerlo mediante Python (x,y) o descargar el instalador (.exe) desde aquí
 |
| Sympy |
Para instalar Sympy en Windows podemos hacerlo mediante Python (x,y) o descargar el instalador (.exe) desde aquí
Para Ubuntu y distribuciones derivadas, se puede realizar fácilmente desde la consola con la siguiente instrucción:
sudo apt-get install python-sympy
Si todavía no se tiene instalado numpy, scipy, o matplotlib también es necesario instalarlos:
sudo apt-get install python-dev python-numpy python-scipy python-matplotlib
Si luego podemos realizar en Python un simple
import sympy
Quiere decir que todo esta listo para trabajar.
FUNCIÓN CUADRADA
El objetivo de este ejercicio es representar una señal cuadrada como una suma de señales sinusoidales y cosinusoidales haciendo uso de la serie trigonométrica de Fourier.
Gráfica de la señal cuadrada
import numpy as np
from scipy import signal as sp
import matplotlib.pylab as plt
amplitud = 1
periodo = np.pi
t = np.arange(-1, 10, 0.001)
funcion = ((sp.square(2 * t)) * (amplitud / 2.0)) + (amplitud / 2.0)
plt.plot(t, funcion, lw=2)
plt.grid()
plt.annotate('Pi', xy = (np.pi, 1), xytext = (np.pi, 1.1))
plt.annotate('Pi/2', xy = (np.pi / 2.0, 1), xytext = (np.pi / 2.0, 1.1))
plt.ylabel('Amplitud')
plt.xlabel('Tiempo(t)')
plt.ylim(-1,2)
plt.xlim(-0.5, 4)
plt.show()
Los coeficientes  ,
,  y
y  son los coeficientes de Fourier y sus valores se pueden hallar de la siguiente manera:
son los coeficientes de Fourier y sus valores se pueden hallar de la siguiente manera:
 ,
,  y
y  son los coeficientes de Fourier y sus valores se pueden hallar de la siguiente manera:
son los coeficientes de Fourier y sus valores se pueden hallar de la siguiente manera:La función que representa la señal cuadrada, esta definida de la siguiente manera:
Eso quiere decir que las formulas de los coeficientes quedan de la siguiente manera:
#Importamos todo el modulo sympy from sympy import * #ademas importamos las variables simbolicas 'n' y 't' from sympy.abc import t, n ao = integrate(2 / pi, (t, 0, pi / 2)) #integramos la funcion (2/pi) cuya variable es 't' #y limites de integracion entre 0 y pi/2 print "a0 = " pprint(ao) #Usamos la funcion pprint para mostrar ao an = integrate((2 / pi) * cos(2 * n * t), (t, 0, pi / 2)) #integramos la funcion (2/pi)*cos(2nt) #Su variable es 't' y sus limites de integracion son 0 y pi/2 print "an = " pprint(an) #Usamos la funcion pprint para mostrar an bn = together(integrate((2 / pi) * sin(2 * n * t), (t, 0, pi / 2))) #integramos la funcion (2/pi*cos(2nt) #Su variable es 't' y sus limites de integracion #son 0 y pi/2. Ademas usamos la funcion "together" #para simplificar la expresion print "bn = " pprint(bn) #Usamos la funcion pprint para mostrar bn
Como resultado, obtenemos lo siguiente:
a0 =
1
an =
sin(π⋅n)
────────
π⋅n
bn =
1 - cos(π⋅n)
────────────
π⋅n
Como podemos ver, la función pprint (pretty print) nos genera una salida con la forma de una ecuación matemática.
Ahora que tenemos los coeficientes de la serie de Fourier vamos a completar la serie usando 7 valores para "n" (el numero "n" son numero enteros que van a ser múltiplos de la frecuencia fundamental. En otras palabras, la cantidad de armónicos con la que vamos a tratar de reconstruir la función inicial)
print "f(x) = " serie=(ao/2)+\ ((an*cos(2*n*t)).subs(n,1))+ \ ((an*cos(2*n*t)).subs(n,2))+ \ ((an*cos(2*n*t)).subs(n,3))+ \ ((an*cos(2*n*t)).subs(n,4))+ \ ((an*cos(2*n*t)).subs(n,5))+ \ ((an*cos(2*n*t)).subs(n,6))+ \ ((an*cos(2*n*t)).subs(n,7))+ \ ((bn*sin(2*n*t)).subs(n,1))+ \ ((bn*sin(2*n*t)).subs(n,2))+ \ ((bn*sin(2*n*t)).subs(n,3))+ \ ((bn*sin(2*n*t)).subs(n,4))+ \ ((bn*sin(2*n*t)).subs(n,5))+ \ ((bn*sin(2*n*t)).subs(n,6))+ \ ((bn*sin(2*n*t)).subs(n,7)) pprint(serie)
esta parte del código realiza la sumatoria que se encuentra en la serie de Fourier usando 7 valores de n.
Primero se toma un valor de "an" y se multiplica por cos(2nt). El ".sub(n,1)" se usa para reemplazar en la función el valor de n por el numero especificado y por ultimo se realiza lo mismo con "bn".
Aunque este código funciona, no es la mejor forma para realizarlo ya que por cada armónico que quisiéramos incluir deberíamos agregar una nueva linea por lo que lo mejor seria hacer algo así:
print "f(x) = "
armonicos = 7
serie = (ao/2)
for i in range(1, armonicos + 1):
serie = serie + (an*cos(2*n*t)).subs(n, i)
for j in range(1, armonicos + 1):
serie = serie + (bn*sin(2*n*t)).subs(n, j)
pprint(serie)
De esa manera podemos definir el número de armónicos de una manera mas sencilla. (en la función range puse la expresión "armonicos + 1" ya que range(1,n) genera una lista desde 1 hasta n-1 )
Al final la serie trigonométrica de Fourier queda de la siguiente manera:
De esta serie podemos notar varias cosas:
1) El termino "1/2" es el resultado de "ao/2". Este termino es conocido como el offset de la señal, y era de esperarse que en una señal cuadrada con un ciclo del 50% con una amplitud de 1 tenga un offset de 0.5.
2) La serie solo contiene términos en función de senos y ningún coseno. Eso quiere decir que el coeficiente "an" es igual a cero para cualquier "n". Sabemos que:
an =
sin(π⋅n)
────────
π⋅n
Si nos fijamos, sin(π⋅n) va a ser igual a cero para cualquier valor de "n" (n pertenece a los números enteros: 1,2,3,4,5...)
3) A pesar de que usamos 7 valores enteros para "n" (1,2,3,4,5,6,7). Solo obtuvimos 4 términos sin contar el offset (ya que este se debe a "ao" y no a "an" o "bn"). Esto se debe a que "bn" es igual a cero cuando "n" es un numero par.
bn =
1 - cos(π⋅n)
────────────
π⋅n
Cuando n toma valores pares (2,4,6), "bn" es igual a cero. Por lo tanto, "bn" solo toma 4 valores que corresponden a los 4 números impares que le asignamos a "n".
4) Entre mas alto sea "n" cada termino va a tener un frecuencia mas alta, pero un amplitud mas baja.
La gráfica de cada uno de los componentes muestras como cada termino tiene mas frecuencia pero menos amplitud
Y la suma de esas 5 gráficas da como resultado la siguiente:
Podemos notar que la suma de esas 5 componentes van formando una señal que se va pareciendo a la señal cuadrada original. Entre mas términos o armónicos (valores de "n") tomemos, la suma de las señales cada vez se va a parecer mas a la señal cuadrada original.
Por ejemplo esta es la gráfica resultante con 100 armónicos
Y esta es la gráfica con 1000 armónicos
Este es la versión final del código:
#!/usr/bin/python
# -*- coding: utf-8 -*-
#Importamos todo el modulo sympy
from sympy import *
#ademas importamos las variables simbolicas 'n' y 't'
from sympy.abc import t, n
ao = integrate(2 / pi, (t, 0, pi / 2))
#integramos la funcion (2/pi) cuya variable es 't'
#y limites de integracion entre 0 y pi/2
print "\n"+"a0 = "
pprint(ao)
#Usamos la funcion pprint para mostrar ao
an = integrate((2 / pi) * cos(2 * n * t), (t, 0, pi / 2))
#integramos la funcion (2/pi)*cos(2nt)
#Su variable es 't' y sus limites de integracion son 0 y pi/2
print "\n"+"an = "
pprint(an)
#Usamos la funcion pprint para mostrar an
bn = together(integrate((2 / pi) * sin(2 * n * t), (t, 0, pi / 2)))
#integramos la funcion (2/pi*cos(2nt)
#Su variable es 't' y sus limites de integracion
#son 0 y pi/2. Ademas usamos la funcion "together"
#para simplificar la expresion
print "\n"+"bn = "
pprint(bn)
#Usamos la funcion pprint para mostrar bn
print "\n"+"f(x) = "
armonicos = 100
serie = (ao/2)
for i in range(1, armonicos + 1):
serie = serie + (an*cos(2*n*t)).subs(n, i)
for j in range(1, armonicos + 1):
serie = serie + (bn*sin(2*n*t)).subs(n, j)
pprint(serie)
plotting.plot(serie, ylim=(-0.5, 1.5), xlim=(-0.5,5)) #Usando el modulo para graficas de sympy


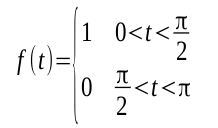






Felicitaciones por tu blog, me ayudo. Gracias.
ResponderEliminarjusto lo que andaba necesitando.
ResponderEliminarExcelente blog, muy bien explicado!
practicamente no hay info en español!
gracias por el esfuerzo!!
¿ en la primer celda de código para el primer comando que usa con el fin de graficar la función cuadrada, que es o para que sirve lo que usted pone allí como lw=2 ?
ResponderEliminar¿ como segunda instancia me gustaría saber si usted de pronto conoce algún comando que me sirve para pedir un ingreso tanto de datos numéricos como funciones ?
es el tamaño de las lineas de la figura si lo aumentas se colocan mas gruesas y viceversa
Eliminarayuda me dice en el codigo final que File "furier.py", line 47, in
ResponderEliminarplotting.plot(serie, ylim=(-0.5, 1.5), xlim=(-0.5,5)) #Usando el modulo para graficas de sympy
AttributeError: 'module' object has no attribute 'plot' como lo soluciono?
muy buen blog gracias por el aporte me sirvio muchisimo sigue asi
ResponderEliminarlo voy a probar, si funciona te aviso :D Gracias por la esperanza...
ResponderEliminarSolo se agrega los parentesis para la versión reciente de python.
ResponderEliminarSaludos
GRACIAS MUCHAS GRACIAS
ResponderEliminarbro sigues ahi ?
ResponderEliminarbuen material ... felicitaciones !!
ResponderEliminar